F1.1 Déterminer différentes façons d’arriver au même montant d’argent en monnaie canadienne jusqu’à 200 ¢ avec diverses combinaisons de pièces de monnaie, et jusqu’à 200 $ avec différentes combinaisons de pièces de 1 $ et de 2 $ et de billets de 5 $, 10 $, 20 $, 50 $ et 100 $.
Activité 1 : la course des lapins
Le but de cette activité consiste à représenter, à l’aide de la droite numérique, un même montant d’argent de différentes façons. Les élèves sont en équipes de 2 ou 3 et chacun de ceux-ci se voit attribuer un lapin qui fera les sauts représentant les combinaisons possibles. Expliquer d’abord aux élèves que chaque lapin doit se rendre au même montant d’argent déterminé en ramassant des cents ou des dollars à chaque bond qu’il fera sur la droite numérique. Chaque lapin devra faire un parcours différent tout en arrivant au même montant d’argent. Les élèves devront représenter les bonds et indiquer les montants d’argent accumulés à chaque bond sur la droite numérique. Chaque parcours aura son lapin et donc sa couleur. Les équipes pourront discuter et observer les différentes courses de lapins.
Exemple
Je dois me rendre au montant de 39 $.
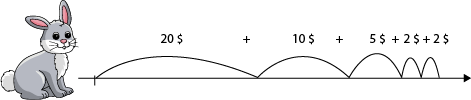
Je prends le billet ou la pièce de monnaie dont la valeur est indiquée à chaque bond, donc un billet de 20 $, un billet de 10 $, un billet de 5 $ et deux pièces de 2 $.

Activité 2 : as-tu la monnaie exacte?
Distribuer aux élèves de petites cartes ayant une friandise glacée et un prix pour chacune, par exemple la sucette glacée vaut 80 ¢ et le cornet de crème glacée vaut 2 $ et ainsi de suite. Varier les sortes de friandises glacées afin d’avoir plusieurs montants différents à représenter. Demander aux élèves de discuter entre eux et de démontrer des combinaisons de pièces de monnaie afin de représenter le montant d’une friandise glacée, de plusieurs différentes façons. Pour complexifier l’activité, distribuer deux ou trois cartes de friandises glacées pour trouver le coût total et ensuite trouver de nouvelles combinaisons et représenter différemment ce plus gros montant d’argent.
Exemple
Je veux acheter la sucette glacée qui vaut 80 ¢.
Voici la combinaison de pièces de monnaie que j’utilise pour représenter la valeur de la sucette glacée. J’ai utilisé deux pièces de 25 ¢ et trois pièces de 10 ¢.

\(25 \ ¢ + 25 \ ¢ + 10 \ ¢ + 10 \ ¢ + 10 \ ¢ = 80 \ ¢ \)
Je peux aussi échanger 1 pièce de 25 ¢ pour 2 pièces de 10 ¢ et 1 pièce de 5 ¢. La nouvelle combinaison serait alors de 1 pièce de 25 ¢, de 5 pièces de 10 ¢ et de 1 pièce de 5 ¢.

\(25 \ ¢ + 10 \ ¢ + 10 \ ¢ + 10 \ ¢ + 10 \ ¢ + 10 \ ¢ + 5 \ ¢ = 80 \ ¢ \)
