F1.1 Identify different ways of representing the same amount of money up to Canadian 200¢ using various combinations of coins, and up to $200 using various combinations of $1 and $2 coins and $5, $10, $20, $50, and $100 bills.
Activity 1: The Rabbit Race
The purpose of this activity is to represent, using the number line, the same amount of money in different ways. Students are divided into groups of 2 or 3 and each group is assigned a rabbit that will make the jumps representing the possible combinations. First explain to the students that all bunnies must get to the same amount of money by collecting dollars and cents with their hops, but that each bunny must make a unique journey. Each bunny will have to make a different journey while arriving at the same amount of money. Students will have to represent the hops and indicate the amount of money accumulated at each hop on the number line. Each rabbit will have its own route and therefore its own colour. Groups can discuss and observe the different bunny routes.
Example
I need to get to $39.
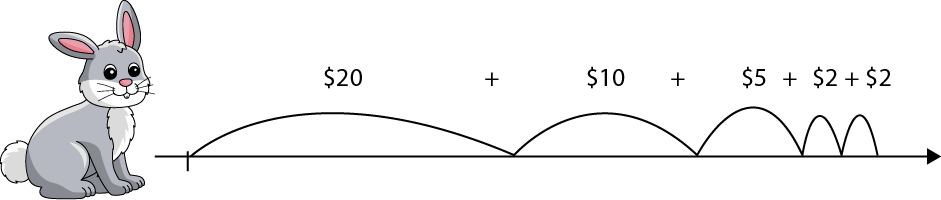
I can represent the red bunny, so as $20, $10, $5 and two $2 + $2.

Activity 2: Do You Have the Exact Change?
Hand out small cards with a special treat and the price it’s worth – for example, a popsicle worth 50¢ and an ice cream cone worth $2 and so on. Vary the types of treats so that there are several different amounts to represent. Have students discuss and demonstrate combinations of coins to represent the amount of an ice cream treat in several different ways. To make the activity more complex, hand out two or three ice cream treat cards and ask the students to find the total cost and different combinations to represent that amount of money.
Example
I want to buy the 80¢ popsicle.
Here is the coin combination I used to represent the value of the popsicle. I used two quarters and three dimes.

\(25¢ + 25¢ + 10¢ + 10¢ + 10¢ = 80¢ \)
I can also exchange 1 quarter for 2 dimes and 1 nickel. The new combination would be 1 quarter, 5 dimes, and 1 nickel.

\(25¢ + 10¢ + 10¢ + 10¢ + 10¢ + 10¢ + 5¢ = 80¢ \)
