F1. Money and Finances
Demonstrate an understanding of the value of Canadian currency.
Learning Situation: The Mysterious Money Bank
Duration: approximately 50 minutes
Overview
In this learning situation, students learn to group and count coins and Canadian bills, forming different combinations that add up to a specific amount of money.
|
Overall Expectation |
Specific Expectation |
|
F1. Financial Literacy Demonstrate an understanding of the value of Canadian currency. |
F1.1 Identify different ways of representing the same amount of money up to Canadian 200¢ using various combinations of coins, and up to $200 using various combinations of $1 and $2 coins and $5, $10, $20, $50, and $100 bills. |
| Preferred High-Impact Mathematics Instructional Practices | Description |
|---|---|
|
Learning Goals, Success Criteria and Descriptive Feedback |
Before beginning this learning situation, it is essential to make the learning goals, based on the curriculum expectations and content, explicit so that they are known and understood by all students. This will ensure that students are aware of the learning goals of the lesson. The success criteria can then be developed and understood through a variety of instructional strategies, such as using examples of student work, co-constructing the success criteria or self-assessing how the criteria have been met. These strategies allow for student engagement and a shared understanding of the steps needed to achieve the learning goals. It is important to make the learning goals and success criteria visible by posting them in the classroom for students to refer to throughout the lesson. Descriptive feedback related to the criteria provides the specific information students need to achieve the intended learning goals. By providing descriptive feedback on multiple occasions, educators help students develop the skills to assess their own learning and reflect on the criteria. In this learning situation, a good time for descriptive feedback is during the Active Learning phase. Students model different combinations of a given amount of money. Students work and communicate in small groups, and, with thoughtful questioning, educators check for understanding and direct students to the criteria to adjust or justify their work. During the Review phase, some solutions may require descriptive feedback from the educator to ensure that the student has the necessary support to revise their thinking to apply to a new context. |
|
Problem-Solving Tasks and Experiences |
This learning situation, where the student must make several combinations of Canadian currency, is a problem-solving experience, as it gives students the opportunity to reason, communicate, represent, make connections, and justify thinking. This learning situation has many entry points and all students will be able to participate and propose solutions using their strategies, as well as their critical and creative thinking. This approach promotes accessibility for all students and the exchange of a variety of mathematical strategies and ideas. This learning situation can be differentiated by using different numbers for the work teams (smaller numbers for a less complex exercise or larger numbers for a more complex exercise), making the task accessible yet challenging for the students. |
|
Math Conversations |
By planning lessons like this, which emphasize collaboration and groupwork, the math conversations are ongoing. These conversations allow students to express themselves and react to the mathematical ideas presented. The role of educators will be to ask open-ended, thought-provoking questions to stimulate thinking and allow for multiple responses. This interaction through questioning must be carefully planned to highlight key concepts, skills, or specific representations to promote student progress. Educators are encouraged to anticipate students' questions and answers in order to make the exercise even more strategic (for example, by anticipating some common errors). As soon as the learning situation begins, educators should ask questions that are accessible to all students and encourage them to share their ideas in the class group. As students are engaged in solving the problem, questioning and discussion should promote their reasoning and justification as a group and develop their critical thinking. During Review, the questioning should support rich mathematical conversation in the whole group and provide educators with the opportunity to assess student understanding of the concepts being learned. |
|
Flexible Groupings |
Flexible groupings can foster collaboration and give students the opportunity to participate in rich math
conversations, learn from each other, and evolve their mathematical thinking. These structures allow
students to work independently of the educator, while benefiting from the support of their peers. It is the
intentional combination of large group, small group, pair, and individual work that can foster a rich
mathematical learning environment. For this learning situation, the initial scenario can be done in a whole
class group. During the Active Learning phase, small groups of two or three are preferable to promote the
participation of each student during the monetary equivalence. Review in the whole class group allows
students to hear the ideas of others, |
Prior Knowledge and Skills
To be able to complete this learning situation, students must be able to:
- Skip count to 200 by 1s, 2s, 5s, 10s, 25, and 100s.
- Read, represent, compose and decompose whole numbers from 0 to 200.
- Use the properties of addition and recall addition facts for numbers up to 20.
- Use equalities to represent, describe, and solve situations involving the addition of whole numbers that sum to 100 or less.
Learning Goals
At the end of this learning situation, students will be able to find different combinations of coins and Canadian dollar bills to represent an amount of money in different ways.
Possible Success Criteria Based on the Achievement Chart
| Skill | Success Criteria |
|---|---|
|
Knowledge and Understanding |
The student understands the equivalence relationships between two combinations of coins or bills that represent the same amount of money. |
|
Thinking |
The student chooses strategies for adding coins and bills. |
|
Communication |
The student will communicate their mathematical reasoning using symbols, drawings, explanations, and manipulatives. |
|
Application |
The student skip counts by 5s, 10s and 25s to group the Canadian coins and bills. The student applies strategies for adding coins and bills to represent a variety of possible combinations for different amounts of money. |
Materials
- Canadian play money set
- erasable whiteboard, large paper or other surface for students to record their combinations
- visual support for displaying problem solving (for example, interactive whiteboard, flashcards, paper strips)
- Appendix 1 - Open Number Line
- Appendix 2 - Blank Model
- Appendix 3 - 5¢, 10¢, and 25¢ Coin Models
- Appendix 4 - Models of Bills up to $50 and Coins of $1 and Over
- Appendix - Sofia's Money Bank Coins
Mathematical Vocabulary
buy, add, repeated addition, bills, combination, compose, decompose, skip count, Canadian dollar, save, equivalence, benchmark numbers, coins, quantity, represent, sum, total, value
Before Learning (Warm-Up)
Duration: approximately 20 minutes
Assessment can be carried out through…
Present the scenario below to the students:
Sofia has saved up enough money to buy a surprise at the Dollar Store. When she reaches into her money bank, she finds different coins, but no $2 coin. What combination of coins can she make to get $2?
Ask students to examine the coins in Sofia's money bank.
Here are the coins in Sofia's money bank:

Using Appendices 1 and 2, have students represent the value of the coins above. This gives students a concrete
representation
of the value of the coins.
Ask students questions to stimulate their thinking and encourage them to share their ideas. Possible questioning include:
- Looking at the contents of Sofia's money bank and the models, what do you notice?
- What is similar? What is different?
- Looking at the coins, how could you group them together to count them? Do you know more than one way to count them?
- Looking at the coin models, how could you group them together to count them? Do you know more than one way to count them?
- Looking at the models, you see that $1 = 100¢ and $2 = 200¢. Is it possible to get the amount of $2 from the 5¢, 10¢, 25¢ and $1 coins? How do you know?
- How many different combinations can we make to get a total amount of $2?
- By making different combinations, how can you vary the coins (or models) to represent the same amount (for example, in what ways can you exchange a 25¢ coin)?
- If we have combinations that include multiple coins, does that change the total value? How do you know?
- How can we get the sum of $2 by combining as few pieces as possible? as few models as possible?
- How can we get the sum of $2 by combining as many pieces as possible? as many models as possible?
Active Learning (Exploration)
Duration: approximately 25 minutes
Assessment can be carried out through…
Explain to students that each team will receive the contents of a money bank that is not Sofia's, so the coins and
dollars
will be a mystery! To purchase a surprise at the Dollar Store, teams will need to represent an amount
assigned to them by
the educator (for example, $5, $12, $37, $74, 65¢, 95¢).
Form teams of two or three students
Distribute a quantity of money to students in a small bag to represent the contents of one of the mystery banks.
Distribute a kit of models, Appendices 1-4, to students to help them visualize the value of bills and coins.
Be sure to vary the coins and bills in the small bags to allow for differentiation and to encourage a variety of
strategies
when solving the problem.
Invite students to discuss and find as many combinations as possible that equal the amount of money assigned.
Ask students to record their different combinations.
Circulate, observe and ask questions.
For example:
- Which coins and bills did you group together?
- Why did you choose to group them in this way?
- How did you count them?
- How else can this amount be represented?
- Is it necessary to use all the coins and bills?
|
Possible Observations |
Possible Interventions |
|
Some students have difficulty skip counting (for example, 5s and 25s). |
|
|
The team represents the amount of money using the same coins without varying them in different combinations (for example, 10 dimes, 4 quarters). |
|
|
The team has difficulty adding up the coins or bills that are part of the chosen combination. |
|
Possible Answer
A team receives a mystery bag containing:

The team must represent a $12 amount with the coins in their mystery bag. The team can use the models to represent the coins.
Through discussion, estimation, calculation, and the use of manipulatives, students could represent the value of the coins as:
5 $2 coins and 2 $1 coins = $12
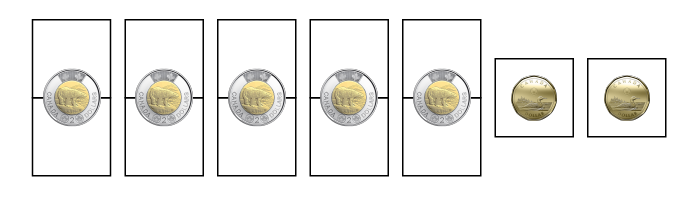
4 $2 coins and 4 $1 coins = $12
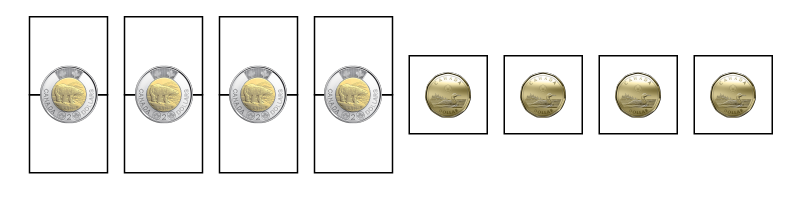
3 $2 coins and 6 $1 coins = $12
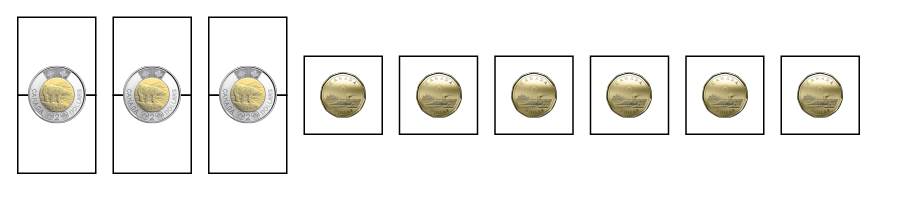
2 $2 coins, 6 $1 coins, 4 25¢ coins, 10 10¢ coins = $12
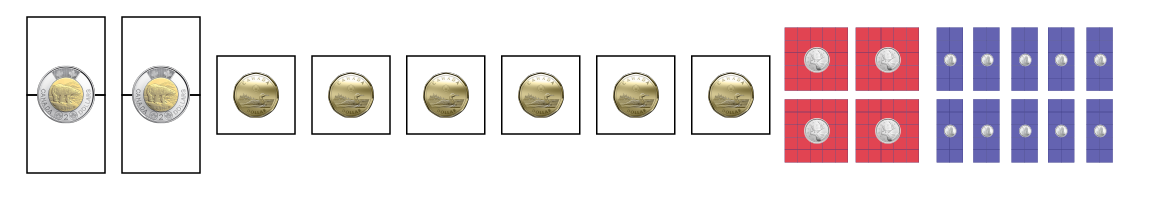
2 $2 coins, 7 $1 coins, 4 25¢ coins = $12

2 $2 coins, 7 $1 coins, 10¢ coins = $12
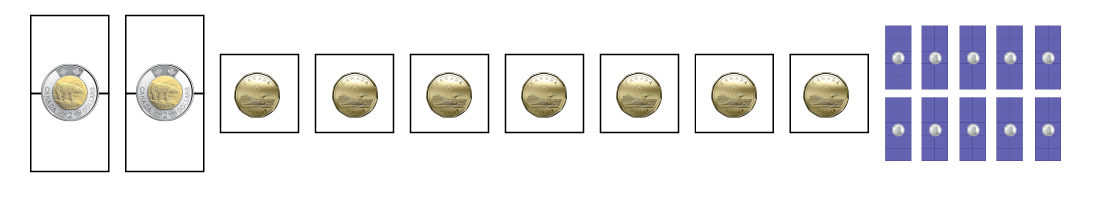
1 $2 coin, 7 $1 coins, 4 25¢ coins, 15 10¢ coins and 10 5¢ coins = $12.

Two squares represent 2 dollars, repeated once, and a one dollar square repeated 7 times. A block of 25 red squares represents a quarter, repeated 4 times. A block of ten blue squares represents a dime, repeated 15 times. A block of 5 yellow squares, represents a nickel, repeated ten times.
Note: Support students to notice regularities in the exchange of coins to create different combinations (for
example, to replace a
$2 coin, I need 2 $1 coins). These relationships relate to content C1.4 in the Algebra
strand.
Review
Duration: approximately 10 minutes
Assessment can be carried out through…
When the students have exhausted the possibilities, ask them to circulate to observe the amounts and combinations of the other teams in order to compare the representations.
Ask students questions to deepen their thinking:
- Why do you think it is important to be able to make several combinations to represent an amount of money?
- In your opinion, when purchasing a good or service, is it better to use as many coins and bills as possible or as few coins and bills as possible?
- Looking at the various representations of other teams, what are the similarities and differences?
- What strategy would you like to use next time? Explain why.
- Which representation or strategy do you think is most effective? Explain why.
- Do you feel you have met the learning goals?
- How did you feel during the teamwork? What emotions did you experience? What strategies could you use in future teamwork to have an even more positive experience?
Review with students that the total value is always the same no matter how many coins are combined. The important thing is to recognize the value of the coins and see how they can be combined to make the same amount. Using the models allows the student to visualize the values of the coins and therefore the amount of money to be represented.
Consolidation of Learning
- Have each group of students choose an amount for another group to represent using play money. Have the groups make a few combinations first to make sure there are enough varied coins in the money bank for the given amount.
- On the interactive whiteboard, show food or objects that students are familiar with, such as fruit, snacks, educational games, or other items. Have groups of students guess the price of the object, then have them choose the coins and bills needed to pay for it. Next show the price of the food or object. Have groups use a variety of combinations to match this amount. Have students walk around the classroom to see the different possible combinations for the same amount.
Links to Other Curriculum Expectations
Number
B1.1 Read, represent, compose, and decompose whole numbers up to and including 200, using a variety of tools and strategies, and describe various ways they are used in everyday life.
B1.4 Count to 200, including by 20s, 25s, and 50s, using a variety of tools and strategies.
B2.2 Recall and demonstrate addition facts for numbers up to 20, and related subtraction facts.
B2.4 Use objects, diagrams, and equations to represent, describe, and solve situations involving addition and subtraction of whole numbers that add up to no more than 100.
Algebra
C1.4 Create and describe patterns to illustrate relationships among whole numbers up to 100.
C2.3 Identify and use equivalent relationships for whole numbers up to 100, in various contexts.
Differentiated Instruction and Universal Design for Learning
- Provide visual supports (reference) for students to identify coins and their value with greater ease.
- Model the task with a small group by representing the monetary equivalencies using concrete models.
- Provide students with a hundreds chart, Rekenrek, or other manipulatives that make it easier for them to count.
- Depending on student interest, adapt the learning situation, change the name of the store, and the purchases to be made.
- To facilitate skip counting, initially offer only 5¢ and 10¢ coins to some teams or $1 coins, $5, and $10 bills, making connections to the 5 and 10 benchmarks on number lines or hundreds charts, for example.
For an Extra Challenge
- Offer only certain coins or bills to represent different amounts of money (develop students' thinking skills).
- Encourage students to do mental math and have them validate their answers using the concrete materials.
- Encourage students to explore and use various manipulatives to represent the same amount of money.
